안녕하세요.
오늘의 파이썬 코딩 독학 주제는 선형회귀입니다.
머신러닝을 공부하시다 보면 무조건 보게되는 단어가 바로 선형회귀입니다.
그렇다면 이 선형회귀는 무엇이고, 왜 머신러닝에 이리 많이 등장하는지에 대해 알아보도록 하겠습니다.
1. 선형회귀(linear regression)란?
가장 기본적인 머신러닝 모델 중 하나로써
오차들의 평균이 가장 작은 직선을 찾는 과정을 뜻합니다.
아래 그림에서
빨간색 점들이 실제 데이터이고
파란색 선과 실제 데이터들 사이의 거리가 오차이며
이 오차들의 평균값을 비용(Cost)이라고 부릅니다.
마지막으로 비용이 가장 작아지도록 그은 선이 그림의 파란색 선입니다.

수식은 아래와 같습니다.
y = W * X + b
혹시 딥러닝 포스팅에서 설명드렸던 식[y = F (W * X + b)]이 떠오르시나요?
딥러닝 식에서 활성화 함수에 대한 항을 뺀 식이 바로 선형회귀 함수의 수식입니다.
2. 선형회귀의 예시
위에서 살펴본 선형회귀의 이론은 생각보다 이해하기 쉬우셨을 겁니다.
그렇다면 대체 이걸 어떻게 머신러닝에 응용할 수 있는걸까요?
선형회귀의 목적은 비용의 최소값을 얻는 것이라고 했습니다.
그를 얻기위한 함수를 비용함수(cost function)이라고 하는데
결국 최적의 W(가중치)와 b(편향)값을 구하는 과정이라고 할 수 있습니다.
머신러닝에서는 이 W와 b를 계속 바꿔가며 학습을 진행하며
학습의 결과물을 토대로 미지의 상황을 예측하게 됩니다.
예를 들면
한 학생이 10분간 공부를 하면 10점의 점수를 얻고,
20분간 공부를 하면 20점의 점수를 얻고,
30분간 공부를 하면 30점의 점수를 얻는다고 했을때
우린 이 학생이 40분간 공부를 하면 40점의 점수를 얻을 수 있을 것이라고 예측할 수 있습니다.

이러한 예측이 가능했던 이유는
우리가 10분, 20분, 30분간의 공부로 받을 수 있는 점수들을 알고 있었기 때문입니다.
머신러닝의 원리 역시 이와 같습니다.
데이터(10분, 20분, 30분간의 공부로 받을 수 있는 점수들)를 통해 학습을 하고,
학습의 결과를 통해 미지의 상황(40분 공부했을때의 점수)을 예측하는 것입니다.
3. 경사하강법(gradient descent)
경사하강법은 비용함수를 최소화 하는 과정에 사용하는 알고리즘입니다.
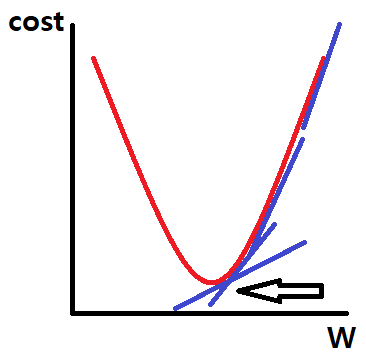
위 그림을 보시면 붉은 그래프의 경사를 따라 파란색 기울기가 점차 작아지는 방향으로 내려가는데,
기울기가 작아지다가 0이 되는 점이 바로 비용함수가 최소인 지점입니다.
이같은 과정을 최적화(optimization)라고 부릅니다.
오늘은 선형회귀에 대해 간단하게 알아보았습니다.
솔직히 저도 아직 뜬구름 잡는 기분이 드는지라
여러분들께 잘 설명이 되고 있는지 잘 모르겠네요.
더 정진하겠읍니다.
'코딩 > 텐서플로우' 카테고리의 다른 글
| 비전공자의 코딩 독학 - 파이썬&텐서플로우(6) <예제2 신경망> (0) | 2020.01.06 |
|---|---|
| 비전공자의 코딩 독학 - 파이썬&텐서플로우(5) <예제1 선형회귀함수> (1) | 2020.01.05 |
| 비전공자의 코딩 독학 - 파이썬&텐서플로우(4) <활성화 함수> (0) | 2019.12.31 |
| 비전공자의 코딩 독학 - 파이썬&텐서플로우(2) <딥러닝> (0) | 2019.12.28 |
| 비전공자의 코딩 독학 - 파이썬&텐서플로우(1) (0) | 2019.12.27 |



